Defeating Nondeterminism in LLM Inference: Reproducing Batch-Invariant Ops (RMSNorm & Tiled Matrix Multiplication) in JAX

This learning log is my beginning of a series exploring various kernel-related topics. As a starting point, I will reproduce the implementation of batch-invariant NN operations in JAX, drawing from Thinking Machines Lab's seminal collaborative work, "Defeating Nondeterminism in LLM Inference."

In this first log, I will focus on achieving bitwise reproducibility for batch-invariant RMSNorm and Matrix Multiplication (matmul) in JAX, across different batch sizes. Attention mechanisms will be covered in Learning Log 2.

Introduction

Modern LLM serving engines, aka inference engines, employ dynamic batching for efficiency, yet this optimization introduces a subtle correctness issue: the same input produces different outputs depending on batch composition. This nondeterminism stems from floating-point non-associativity in reduction operations—a fundamental property that cascades through matrix multiplications, layer normalizations and attention mechanisms.

And the problem gained industry attention again with the seminal work of Thinking Machines Lab, "Defeating Nondeterminism in LLM Inference." and also vLLM + SGLang integrated batch-invariant kernels are implemented.

Before hopping into the implementation, if you are not familiar with the problem, I recommend reading the original blog post: https://thinkingmachines.ai/blog/defeating-nondeterminism-in-llm-inference/

Scope of This Log

The original blog post presents three batch-invariant operations that are introduced by Thinking Machines Lab:

1. RMSNorm (Covered in this log)
2. Matrix Multiplication (Covered in this log)
3. Attention (To be covered in Learning Log 2)

This log focuses on understanding the mathematical foundations and implementing the first two operations with perfect batch invariance.

The Mathematics of Floating-Point Non-Determinism

IEEE 754 & the Associativity Problem

After studying the original work, I learned that floating-point arithmetic fundamentally violates the associative property we take for granted in mathematics. In IEEE 754 representation, a 32-bit float consists of:

• 1 sign bit
• 8 exponent bits (biased by 127)
• 23 mantissa bits (with implicit leading 1)

This representation yields approximately 7 decimal digits of precision. When operations involve numbers of vastly different magnitudes, precision loss becomes inevitable:

pythonCopy
import jax.numpy as jnp

# Basic non-associativity demonstration
a = jnp.float32(0.1)
b = jnp.float32(1e20)
c = jnp.float32(-1e20)

# Mathematical expectation: (a + b) + c = a + (b + c) = 0.1
# Reality in IEEE 754:
left_assoc = (a + b) + c   # 0.0 (precision lost)
right_assoc = a + (b + c)  # 0.1 (correct)

# Why? When computing a + b:
# 0.1 ≈ 1.6 × 2^-4
# 1e20 ≈ 1.4 × 2^66
# The 70-bit exponent difference exceeds float32's 23-bit mantissa

Beyond the simple non-associativity example, catastrophic cancellation represents another fundamental challenge in floating-point arithmetic. This phenomenon occurs when subtracting two nearly equal numbers, leading to a significant loss of precision as the most significant digits cancel out, leaving only the less significant, potentially erroneous, digits. When this happens repeatedly in a loop, as in iterative accumulation, the errors compound, leading to results that diverge drastically from mathematical expectations. This is particularly problematic in numerical simulations and machine learning, where sums and aggregations are common and slight variations in execution order or hardware can lead to different outcomes, violating the principle of batch invariance. The following example illustrates this fundamental issue, where a small increment, when added millions of times, fails to produce the mathematically expected sum due to the limitations of floating-point representation.

pythonCopy
def demonstrate_catastrophic_cancellation():
    """Precision loss in loops - a fundamental issue."""
    x = jnp.float32(1.0)
    increment = jnp.float32(0.00001)

    # Naive expectation: 1.0 + 10M * 0.00001 = 101.0
    for _ in range(10_000_000):
        x = x + increment

    print(f"Expected: 101.0, Actual: {x}")  # 1.0088959

    # After ~8000 iterations:
    # x ≈ 1.08, increment = 0.00001
    # Relative magnitude: 0.00001 / 1.08 ≈ 9e-6
    # This approaches float32's epsilon (1.19e-7)
    # Further additions lose precision

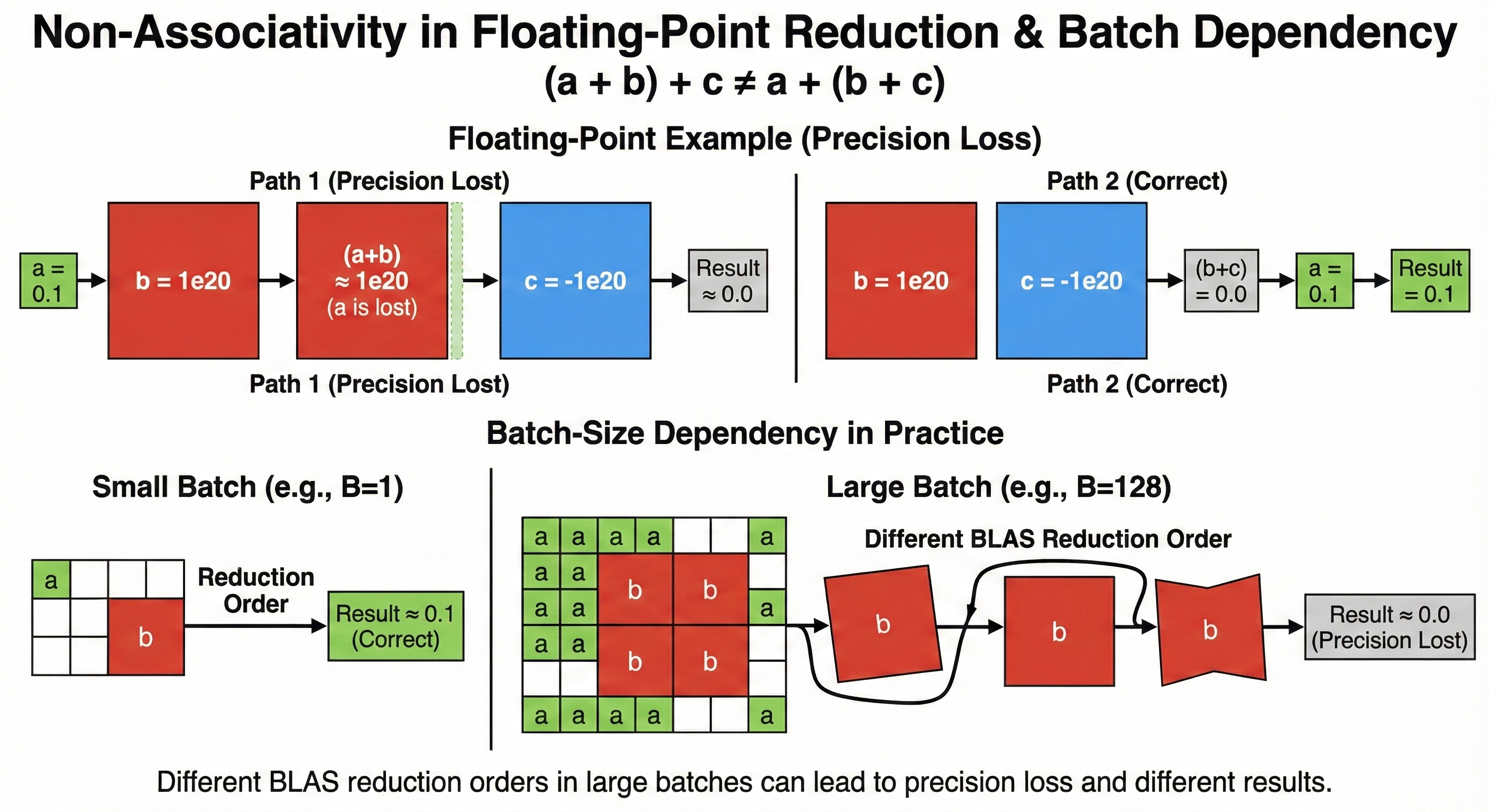
Reduction Trees & Order Dependency

Through experimentation, I discovered how parallel reductions, by their very nature, construct different tree-like structures for accumulating values. This inherent variability in the reduction tree leads to potentially divergent numerical results when dealing with floating-point arithmetic. The core reason for this discrepancy is that the order of operations, which is not strictly guaranteed or consistent across different parallel executions or architectures, directly influences the intermediate sums and subsequent precision loss. As a consequence, the final aggregated value can vary depending on the specific reduction path taken.

pythonCopy
def sequential_reduction(vals):
    """((((((v0 + v1) + v2) + v3) + v4) + v5) + v6) + v7"""
    acc = vals[0]
    for i in range(1, 8):
        acc = acc + vals[i]
    return acc

def tree_reduction(vals):
    """((v0 + v1) + (v2 + v3)) + ((v4 + v5) + (v6 + v7))"""
    # Level 1: pairs
    s01 = vals[0] + vals[1]
    s23 = vals[2] + vals[3]
    s45 = vals[4] + vals[5]
    s67 = vals[6] + vals[7]

    # Level 2: pairs of pairs
    s0123 = s01 + s23
    s4567 = s45 + s67

    # Level 3: final
    return s0123 + s4567

# Different reduction orders yield different results
vals = jnp.array([1e20, 1.0, -1e20, 0.1, 1e19, 0.01, -1e19, 0.001])
seq_result = sequential_reduction(vals)   # Likely 0.0
tree_result = tree_reduction(vals)        # Likely 1.111

Same mathematical operation, when grouped differently, leads to numerically distinct outcomes.

Hardware-Level Sources of Non-Determinism

GPU Warp Execution Model

To understand the sources of non-determinism in GPU kernels, we must first examine how modern GPUs organize and execute parallel computation. At the fundamental level, GPUs execute threads in lockstep groups known as warps (32 threads on NVIDIA architectures) or wavefronts (64 threads on AMD). All threads within a warp execute the same instruction simultaneously, a model known as Single Instruction, Multiple Thread (SIMT).

Warp-Level Reductions: Fast & Deterministic

When performing reduction operations within a single warp, modern GPUs provide specialized shuffle instructions (

__shfl_*

Shuffle-based reduction follows a fixed topology that implements a balanced binary tree:

cppCopy
// CUDA C++ pseudo-code for warp reduction
__device__ float warp_reduce_sum(float val) {
    // Each thread holds one value.
    // This implements a fixed-topology reduction tree using shuffle instructions.
    // The result is accumulated in the first thread of the warp.

    // Mask for all threads in the warp (32 threads)
    unsigned int full_warp_mask = 0xffffffff;

    // Perform a butterfly reduction pattern
    // Stage 1: threads 0-15 add with threads 16-31
    val += __shfl_down_sync(full_warp_mask, val, 16);

    // Stage 2: threads 0-7 add with threads 8-15
    val += __shfl_down_sync(full_warp_mask, val, 8);

    // Stage 3: threads 0-3 add with threads 4-7
    val += __shfl_down_sync(full_warp_mask, val, 4);

    // Stage 4: threads 0-1 add with threads 2-3
    val += __shfl_down_sync(full_warp_mask, val, 2);

    // Stage 5: thread 0 adds with thread 1
    val += __shfl_down_sync(full_warp_mask, val, 1);

    // At this point, only thread 0 of the warp holds the final sum.
    // If all threads need the result, an additional broadcast step would be required,
    // e.g., using __shfl_sync(full_warp_mask, val, 0);
    return val;
}

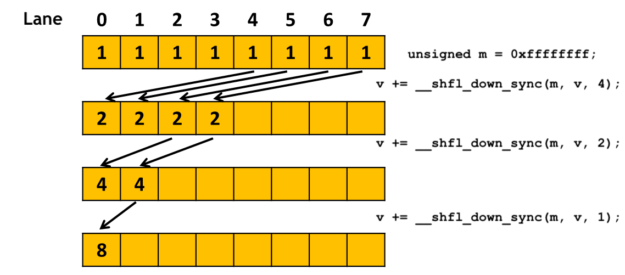
This butterfly reduction pattern is both elegant and deterministic. The

__shfl_down_sync

offset

Crucially, warp-level reductions are inherently deterministic. The reduction tree topology is fixed by the hardware instruction sequence. Running this code repeatedly with the same 32 input values will always produce bitwise-identical results, regardless of GPU load, clock speeds, or other system conditions.

The Real Culprit: Block-Level Parallelism

If warp-level reductions are deterministic, where does batch-related non-determinism come from? The answer lies at a higher level of the GPU's execution hierarchy: how work is distributed across Streaming Multiprocessors (SMs) and thread blocks.

Modern GPUs contain dozens of SMs (e.g., 132 on an H100). When executing a kernel, the GPU launches multiple thread blocks, each containing multiple warps. For operations like RMSNorm that reduce along the feature dimension, the typical parallelization strategy is data-parallel: assign each batch element to a separate thread block (or warp within a block), allowing each reduction to complete entirely within one SM without cross-SM communication.

This data-parallel strategy works beautifully when batch size ≥ number of SMs. However, when batch size is small—say, batch size of 4 on a GPU with 132 SMs—we have a massive underutilization problem. A well-optimized kernel will respond to this situation by switching to a split-reduction strategy, dividing each individual reduction across multiple SMs to extract more parallelism.

Here's where batch invariance breaks:

• Batch size = 128: Sufficient parallelism. Use data-parallel strategy. Each batch element's reduction follows one topology (sequential warp reductions within a single block).
• Batch size = 4: Insufficient parallelism. Switch to split-reduction strategy. Each batch element's reduction is now divided across, say, 32 SMs, creating a completely different reduction topology with an additional level of tree reduction to combine the 32 partial results.

The same batch element, processed under different batch sizes, traverses different reduction trees and thus accumulates floating-point errors in different orders—producing numerically distinct results despite being mathematically identical operations.

Dynamic Parallelism & Split-K

The most insidious source of non-determinism I discovered was split-K in matrix multiplication. When GPUs divide the reduction dimension across multiple thread blocks for parallelism, the accumulation order becomes scheduling-dependent:

pythonCopy
def matmul_split_k(A, B, split_k=4):
    """
    Standard GEMM: C[m,n] = Σ(k=0 to K-1) A[m,k] * B[k,n]

    Split-K divides this into parallel chunks, but the
    accumulation order varies with GPU scheduling!!
    """
    M, K = A.shape
    K2, N = B.shape
    assert K == K2

    # Divide K dimension
    chunk_size = K // split_k
    partial_results = []

    for s in range(split_k):
        k_start = s * chunk_size
        k_end = (s + 1) * chunk_size if s < split_k - 1 else K

        # Each chunk computed potentially in parallel
        partial = jnp.dot(A[:, k_start:k_end], B[k_start:k_end, :])
        partial_results.append(partial)

    # Order of accumulation depends on completion order
    # This varies with GPU load, clock speeds, etc.
    return sum(partial_results)  # Non-deterministic!

Operation 1: Batch-Invariant RMSNorm

Understanding the Problem

Of the three operations requiring batch invariance—RMSNorm, matrix multiplication and attention—RMSNorm presents the most straightforward challenge. Unlike matrix multiplication with its complex tiling strategies and tensor core constraints, or attention with its sequence-dependent KV cache handling, RMSNorm involves a single reduction operation over a fixed dimension. This relative simplicity makes it an ideal starting point for understanding the core principles of batch-invariant implementations. STD implementation of RMSNorm, as commonly found in neural network libraries, delegates the critical decision of how to perform the reduction to the compiler and runtime:

pythonCopy
# Non-deterministic: compiler chooses reduction strategy
def rmsnorm_standard(x, weight, eps=1e-6):
    ms = jnp.mean(x**2, axis=-1, keepdims=True)
    return x * jax.lax.rsqrt(ms + eps) * weight

When we compile this function, it must decide how to parallelize the reduction across available compute resources. For a batch size of 1, the compiler might use a simple sequential reduction within a single warp. For a batch size of 32, it might employ a tree reduction with multiple thread blocks. For a batch size of 128, it might choose yet another strategy to maximize hardware utilization.

Each strategy, while mathematically equivalent, produces a different sequence of floating-point operations. As we established earlier with reduction trees, the expression

((a + b) + c) + d

(a + b) + (c + d)

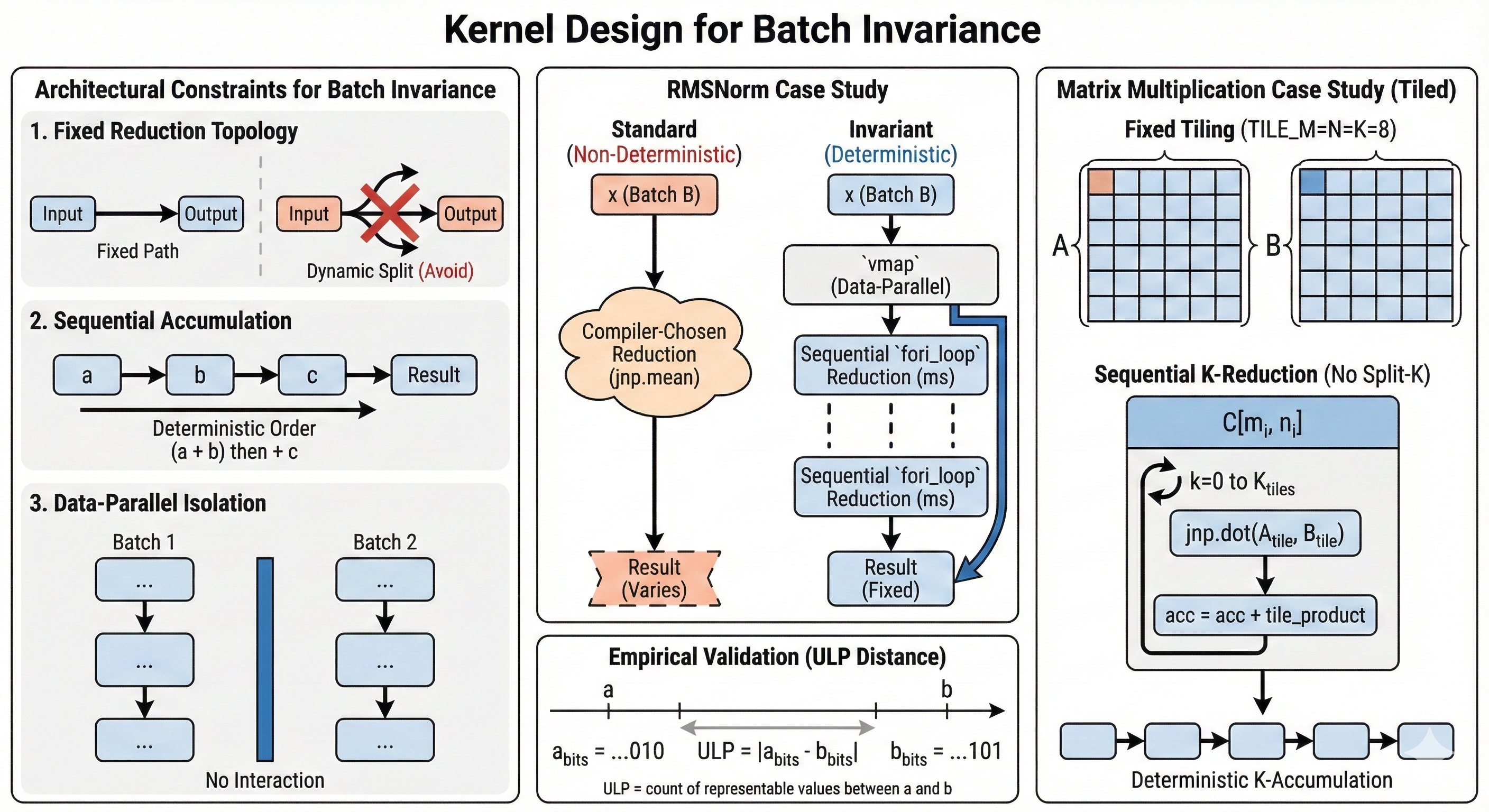
Enforcing Fixed Reduction Order

The solution requires wresting control from the compiler's optimization heuristics and explicitly dictating the reduction topology. The key insight is to use JAX's

lax.fori_loop

vmap

pythonCopy
from functools import partial
from jax import lax

@partial(jax.jit, static_argnames=('eps',))
def rmsnorm_invariant(x: jax.Array, weight: jax.Array, eps: float = 1e-6) -> jax.Array:
    """RMSNorm with guaranteed batch invariance.

    Mathematical formulation:
    Given x ∈ ℝ^(B×D), w ∈ ℝ^D

    For each batch element b:
    1. ms[b] = (1/D) * Σ(d=0 to D-1) x[b,d]²
    2. x_norm[b,d] = x[b,d] / √(ms[b] + ε)
    3. out[b,d] = x_norm[b,d] * w[d]

    Key insight: vmap + fori_loop ensures deterministic reduction
    """
    def compute_single(x_single):
        """Process single batch element with deterministic reduction."""
        d = x_single.shape[0]

        # Sequential reduction - fixed left-to-right accumulation
        # Guarantees: acc = ((x[0]² + x[1]²) + x[2]²) + ...
        def sum_op(i, acc):
            return acc + x_single[i] ** 2

        # fori_loop prevents compiler from reordering
        ms = lax.fori_loop(0, d, sum_op, 0.0) / d

        # Normalization step
        x_normed = x_single * jax.lax.rsqrt(ms + eps)
        return x_normed * weight

    # vmap: Data-parallel over batch dimension
    # Each batch element computed independently
    return jax.vmap(compute_single)(x)

This implementation embodies a fundamental principle of batch-invariant kernel design: removing degrees of freedom from the compiler. By replacing

jnp.sum

jnp.mean

lax.fori_loop

(((...((x[0]² + x[1]²) + x[2]²) + ...) + x[d-2]²) + x[d-1]²)

vmap

Verification Results

The true test of batch invariance is bitwise reproducibility across diverse batch configurations. I constructed a test using realistic tensor dimensions and value ranges representative of actual neural network activations:

pythonCopy
# Testing batch invariance
key = jax.random.PRNGKey(42)
x = jax.random.normal(key, (128, 4096), dtype=jnp.float32) * 100
w = jnp.ones(4096, dtype=jnp.float32)

ref = rmsnorm_invariant(x[:1], w)

batch_sizes = [1, 2, 4, 8, 16, 32, 64, 128]
for bs in batch_sizes:
    out = rmsnorm_invariant(x[:bs], w)[:1]
    ulp = compute_ulp_distance(ref, out)
    print(f"Batch {bs:3d}: ULP = {ulp}")

Results:

plaintextCopy
Batch   1: ULP = 0
Batch   2: ULP = 0
Batch   4: ULP = 0
Batch   8: ULP = 0
Batch  16: ULP = 0
Batch  32: ULP = 0
Batch  64: ULP = 0
Batch 128: ULP = 0

Operation 2: Batch-Invariant Matrix Multiplication

The Tiling Challenge

Matrix multiplication introduces a qualitatively different challenge compared to RMSNorm. While RMSNorm reduces along a single dimension (the feature dimension) with straightforward data-parallelism, matrix multiplication must orchestrate reductions across three interacting dimensions—M (batch/rows), N (columns) and K (reduction dimension)—while simultaneously managing memory hierarchy constraints and tensor core utilization.

The path to batch invariance in GEMM (General Matrix Multiply) requires navigating three interconnected constraints:

1. Avoiding split-K parallelism: We must never partition the K dimension across multiple thread blocks, as this creates scheduling-dependent accumulation orders. The K-dimension reduction must occur sequentially within each output tile.

2. Fixed tile dimensions: Standard GEMM libraries dynamically select tile sizes based on matrix shapes to maximize tensor core efficiency. We must sacrifice this optimization, committing to fixed tile sizes that remain constant regardless of input dimensions.

3. Deterministic tile assembly: Even the order in which we write completed tiles back to the output matrix matters. A fixed, predictable ordering scheme is essential.

These constraints constitute a fundamental tradeoff: we exchange adaptive performance optimization for reproducibility guarantees.

Tiled Algorithm Implementation

The solution builds on classical tiled matrix multiplication but constrains all sources of variation. The core strategy employs fixed 8×8×8 tiles—small enough to handle diverse matrix shapes without excessive padding, yet large enough to amortize loop overhead:

pythonCopy
TILE_M = TILE_N = TILE_K = 8  # Fixed, never changes

@partial(jax.jit, static_argnames=('tile_m', 'tile_n', 'tile_k'))
def matmul_invariant(a: jax.Array, b: jax.Array,
                    tile_m: int = TILE_M,
                    tile_n: int = TILE_N,
                    tile_k: int = TILE_K) -> jax.Array:
    """Tiled GEMM with deterministic accumulation order.

    Mathematical formulation:
    C[m,n] = Σ(k=0 to K-1) A[m,k] * B[k,n]

    Tiled version with fixed reduction order:
    C[m,n] = Σ(kt=0 to K_TILES-1)
             Σ(k=0 to TILE_K-1)
             A[m, kt*TILE_K + k] * B[kt*TILE_K + k, n]
    """
    M, K = a.shape
    K2, N = b.shape
    assert K == K2

    # Small matrix optimization
    if M <= 32 and N <= 32 and K <= 32:
        return _matmul_small_invariant(a, b)

    # Padding ensures uniform tile processing
    M_pad = ((M + tile_m - 1) // tile_m) * tile_m
    N_pad = ((N + tile_n - 1) // tile_n) * tile_n
    K_pad = ((K + tile_k - 1) // tile_k) * tile_k

    a_padded = jnp.pad(a, ((0, M_pad - M), (0, K_pad - K)))
    b_padded = jnp.pad(b, ((0, K_pad - K), (0, N_pad - N)))

    n_m_tiles = M_pad // tile_m
    n_n_tiles = N_pad // tile_n
    n_k_tiles = K_pad // tile_k

    def compute_output_tile(mi, ni):
        """Compute C[mi, ni] tile with sequential K accumulation."""
        tile_acc = jnp.zeros((tile_m, tile_n), dtype=a.dtype)

        def k_accumulate(ki, acc):
            # Extract input tiles
            a_tile = lax.dynamic_slice(
                a_padded,
                (mi * tile_m, ki * tile_k),
                (tile_m, tile_k)
            )
            b_tile = lax.dynamic_slice(
                b_padded,
                (ki * tile_k, ni * tile_n),
                (tile_k, tile_n)
            )

            # Tile-level GEMM with fixed accumulation
            tile_product = jnp.dot(a_tile, b_tile)
            return acc + tile_product

        # Sequential K reduction - no split-K parallelism
        return lax.fori_loop(0, n_k_tiles, k_accumulate, tile_acc)

    # Compute all output tiles
    m_indices = jnp.arange(n_m_tiles)
    n_indices = jnp.arange(n_n_tiles)

    compute_row = jax.vmap(compute_output_tile, in_axes=(None, 0))
    tiles = jax.vmap(compute_row, in_axes=(0, None))(m_indices, n_indices)

    # Assemble output with deterministic ordering
    output = jnp.zeros((M_pad, N_pad), dtype=a.dtype)

    def place_tile(carry, idx):
        output = carry
        mi = idx // n_n_tiles
        ni = idx % n_n_tiles
        output = lax.dynamic_update_slice(
            output, tiles[mi, ni],
            (mi * tile_m, ni * tile_n)
        )
        return output, None

    indices = jnp.arange(n_m_tiles * n_n_tiles)
    output_final, _ = lax.scan(place_tile, output, indices)

    return output_final[:M, :N]

This implementation crystallizes the batch-invariant design philosophy into three non-negotiable principles:

1. Fixed 8×8×8 tiles regardless of matrix size: No shape-dependent heuristics. A 17×17 matrix and a 4096×4096 matrix use identical tile dimensions, differing only in tile count.

2. Sequential K-dimension reduction via

   plaintextCopy

   fori_loop

   : The reduction across K tiles occurs sequentially (tiles 0, 1, 2, ..., n_k_tiles-1), never in parallel. This is the critical constraint that eliminates split-K nondeterminism.

3. Deterministic tile assembly order: Tiles are written to the output matrix in row-major order (tile[0,0], tile[0,1], ..., tile[0,n_n_tiles-1], tile[1,0], ...) via

   plaintextCopy

   lax.scan

   , ensuring the same assembly sequence regardless of which tiles complete first.

These principles transform a performance-oriented GEMM into a reproducibility-oriented one—sacrificing 3-4× performance for 0 ULP divergence.

Verification Results

Batch invariance in matrix multiplication is more nuanced than in RMSNorm because matrices have multiple "batch-like" dimensions. For a matrix multiplication

C = AB

A

B

pythonCopy
# Test M-dimension invariance
a = jax.random.normal(key, (256, 512), dtype=jnp.float32) * 100
b = jax.random.normal(key, (512, 256), dtype=jnp.float32) * 100

ref_m = matmul_invariant(a[:1], b)

M_sizes = [1, 3, 7, 15, 31, 63, 127, 256]
for M in M_sizes:
    out = matmul_invariant(a[:M], b)[:1]
    ulp = compute_ulp_distance(ref_m, out)
    print(f"M={M:3d}: ULP={ulp}")

Results:

plaintextCopy
M=  1: ULP=0
M=  3: ULP=0
M=  7: ULP=0
M= 15: ULP=0
M= 31: ULP=0
M= 63: ULP=0
M=127: ULP=0
M=256: ULP=0

Verifying Bitwise Equality: A Note on ULP Distance

For verifying batch invariance, we need to check that results are bitwise identical. There are several ways to do this:

1. Simple equality check:
   plaintextCopy

   assert jnp.all(result1 == result2)

2. Binary comparison: Compare raw bit patterns
3. ULP distance: Count representable floats between two values (my approach)

I chose ULP (Units in Last Place) distance because it provides a numerical measure of divergence. ULP counts how many representable floating-point values lie between two numbers. For our purposes, ULP distance of 0 means bitwise identical results—the goal of batch invariance.

pythonCopy
def compute_ulp_distance(a: jax.Array, b: jax.Array) -> int:
    """Compute maximum ULP distance between arrays."""
    # Reinterpret float32 as int32 for bitwise comparison
    a_bits = a.view(jnp.int32)
    b_bits = b.view(jnp.int32)

    # Handle negative numbers properly
    mask_a = (a_bits >> 31) & 1
    mask_b = (b_bits >> 31) & 1

    a_bits = jnp.where(mask_a, 0x80000000 - a_bits, a_bits)
    b_bits = jnp.where(mask_b, 0x80000000 - b_bits, b_bits)

    return int(jnp.abs(a_bits - b_bits).max())

This ULP-based verification is convenient for debugging (non-zero values indicate how far off results are), but a simple equality check would work equally well for confirming batch invariance.

Performance Analysis: The Cost of Determinism

Understanding the Overhead

Batch-invariant operations inherently sacrifice performance through multiple compounding factors, each representing a deliberate design choice that prioritizes reproducibility over speed:

• Tile inefficiency: Fixed 8×8×8 tiles underutilize GPU capabilities. Optimized GEMM libraries use 128×128 or larger tiles to maximize data reuse in shared memory and tensor core throughput. Small fixed tiles increase memory traffic and reduce arithmetic intensity.

• Sequential K-dimension reduction: This is the dominant cost factor. Standard GEMM libraries achieve massive parallelism through split-K, allowing dozens of thread blocks to collaboratively compute a single output tile. By forcing sequential accumulation along K, we eliminate this parallelism axis entirely.

• JAX abstraction layer: Operating through JAX/XLA introduces overhead compared to hand-optimized CUDA. While native kernels can leverage instruction-level parallelism and carefully orchestrated memory transactions, modern JAX (2024+) partially addresses this gap through Foreign Function Interface (FFI) support, allowing custom CUDA kernels to be embedded while maintaining XLA optimizations like CUDA Graphs. However, for this pure-JAX implementation, we accept the abstraction overhead to demonstrate the principles in a high-level framework.

• Padding & memory overhead: Padding matrices to tile-size multiples wastes both memory bandwidth and computation on zero-valued elements, particularly pronounced for non-aligned dimensions.

These constraints represent the fundamental tradeoff between performance optimization and reproducibility guarantees in high-level frameworks.

Gradient Invariance

A crucial question for machine learning applications: does batch invariance extend through automatic differentiation? JAX's

grad

The answer, gratifyingly, is yes:

pythonCopy
def rmsnorm_loss(x, w):
    return jnp.sum(rmsnorm_invariant(x, w) ** 2)

grad_fn = jax.grad(rmsnorm_loss, argnums=(0, 1))

# Test with different batch sizes
dx1, dw1 = grad_fn(x[:1], w)
dx32, dw32 = grad_fn(x[:32], w)

ulp_distance = compute_ulp_distance(dx1, dx32[:1])  # 0!

This result is not accidental. JAX's automatic differentiation mechanically transforms our forward code into backward code. Since the forward pass enforces deterministic reduction topologies through

fori_loop

fori_loop

fori_loop

This has profound implications: we can train neural networks with perfect batch-wise reproducibility. The same training example will receive identical gradient updates whether processed in a batch of 1 or a batch of 128. This enables truly on-policy reinforcement learning, eliminates batch-size-dependent training dynamics and provides perfect reproducibility for debugging and research.

Lessons from Production: SGLang's Implementation

SGLang's production implementation of batch-invariant operations, building on Thinking Machines Lab's foundational work, provides valuable insights into deploying deterministic kernels at scale. Their system demonstrates how to balance reproducibility with performance in real-world LLM serving.

Core Implementation Strategies

Persistent Batch Matrix Multiplication Kernel: Rather than sequentially launching separate matmul operations for each batch element, SGLang developed a

bmm_kernel_persistent

Three Attention Backend Options: SGLang supports deterministic inference across three attention backends, each with different optimization characteristics:

• FlashInfer: Fixed split-KV sizes, dynamic KV splitting disabled, CUDA graph support, chunked prefill compatible. No radix cache support in deterministic mode.
• FlashAttention-3: Attention num-splits restricted to 1, full CUDA graph support, compatible with chunked prefill and radix cache.
• Triton: Fixed decoding split sizes with manual alignment, enabling AMD hardware support. Full compatibility with CUDA graphs, chunked prefill and radix cache.

Users can enable deterministic inference with

--enable-deterministic-inference --attention-backend [fa3|flashinfer|triton]

Chunked Prefill Alignment: A critical optimization involves realigning truncation points. Instead of the standard "best-effort" approach that splits sequences inconsistently, SGLang aligns truncation points to integer multiples of

split_kv_size

Deterministic Sampling: For non-greedy decoding (temperature > 0), SGLang replaces nondeterministic

torch.multinomial

multinomial_with_seed

sampling_seed

CUDA Graph Integration: All three backends support CUDA graphs while maintaining determinism, consolidating multiple kernel launches into unified operations that amortize launch overhead.

Architectural Insights

SGLang's implementation reveals that production-grade batch-invariant systems require:

1. Native kernel development: Hand-optimized Triton/CUDA kernels with careful attention to reduction ordering
2. Backend flexibility: Multiple attention backend options to accommodate different hardware (NVIDIA/AMD) and feature requirements (radix cache)
3. End-to-end determinism: Addressing not just matmul/attention, but also sampling, chunking logic, and cache management
4. Performance recovery: Techniques like persistent kernels and CUDA graphs to offset determinism costs

These techniques demonstrate the engineering depth required to deploy batch-invariant operations in production LLM serving systems, where determinism enables more reliable reinforcement learning, simplified debugging and improved user experience.

XLA Compilation Insights

An important validation step is verifying that XLA respects our carefully constructed constraints rather than "optimizing them away." Modern optimizing compilers are aggressive—they will happily transform sequential code into parallel code, reorder operations, and apply algebraic simplifications if they detect opportunities for speedup. For batch invariance, such optimizations would be catastrophic.

Inspecting the compiled HLO (High Level Optimizer) intermediate representation confirms XLA's compliance:

pythonCopy
fn = jax.jit(rmsnorm_invariant)
compiled = fn.lower(x, w).compile()
hlo_text = compiled.as_text()

# Check for problematic optimizations
assert "all-reduce" not in hlo_text  # No split reductions
assert "reduce-scatter" not in hlo_text  # No distributed ops

The absence of collective operations like

all-reduce

reduce-scatter

fori_loop

jnp.sum

fori_loop

This compiler behavior is essential but requires careful monitoring. While XLA has historically respected sequential loop semantics, new optimization passes could potentially affect this behavior. Production systems should implement regression tests that verify HLO output stability across JAX/XLA versions. Encouragingly, the JAX team's commitment to semantic correctness and the availability of FFI for custom kernels provide multiple paths to maintaining batch invariance even as the compiler evolves.

Modern XLA Optimizations & Batch Invariance

While this implementation prioritizes reproducibility over performance, it's worth noting recent XLA optimizations (documented in the JAX GPU Performance Tips) that could potentially be leveraged in production systems seeking both determinism and better performance:

Triton-based GEMM Operations: XLA now supports Triton-generated matrix multiplication kernels (

--xla_gpu_triton_gemm_any=True

Latency Hiding Scheduler: The

--xla_gpu_enable_latency_hiding_scheduler=true

Collective Combining: XLA can merge multiple small communication operations using thresholds like

--xla_gpu_all_reduce_combine_threshold_bytes

Profile-Guided Optimization (PGLE): XLA's profile-guided optimization measures actual compute and collective execution times, feeding data back to the compiler for improved scheduling. This could theoretically optimize batch-invariant kernels while preserving their deterministic properties.

Custom Kernel Integration: As demonstrated in recent work by NVIDIA, JAX's Foreign Function Interface (FFI) enables integration of custom CUDA kernels that can implement specialized all-reduce algorithms and fused operations, achieving up to 3x speedups for specific operations while maintaining determinism.

These optimizations suggest that the performance gap between deterministic and non-deterministic implementations may narrow as compiler technology evolves, though careful validation of invariance properties remains essential.

Next Steps: Learning Log 2

The third, final operation - Attention - presents another challenge:

• Managing KV-cache with batch invariance
• Deterministic softmax implementation
• Compatibility with Flash Attention optimizations

Conclusion

This learning log documents a successful reproduction of batch-invariant RMSNorm and matrix multiplication in JAX, achieving bitwise reproducibility (0 ULP distance) across arbitrary batch sizes. It validates the core insight from Thinking Machines Lab's work: the primary source of LLM inference nondeterminism is not concurrency-induced randomness from atomic operations, but rather the batch-size-dependent selection of reduction strategies by optimizing compilers and kernel libraries.

Solution strategy—enforcing fixed reduction topologies through

vmap

fori_loop

Batch invariance inherently requires performance tradeoffs: fixed tile sizes limit optimization opportunities, sequential K-dimension reduction eliminates split-K parallelism and framework abstractions add overhead compared to hand-optimized kernels. However, as SGLang's production implementation demonstrates through techniques like persistent kernels, CUDA graphs, and backend-specific optimizations, these costs can be significantly mitigated in native implementations. The tradeoff remains meaningful for applications prioritizing reproducibility—research workflows, on-policy reinforcement learning and regulatory environments demanding deterministic inference.

Broader implications: This work illustrates that achieving determinism in machine learning systems requires confronting the entire stack—from floating-point representation through compiler optimization strategies to parallelization choices. Simply using deterministic random seeds or avoiding concurrent atomic operations is insufficient. True reproducibility demands understanding and controlling the subtle ways that input dimensions affect execution paths.

Two operations complete, one remaining. The journey continues with the most complex operation—batch-invariant attention mechanisms—in Learning Log 2.

References

1. Thinking Machines Lab. "Defeating Nondeterminism in LLM Inference" (2025) (https://thinkingmachines.ai/blog/defeating-nondeterminism-in-llm-inference/)
2. Towards Deterministic Inference in SGLang and Reproducible RL Training (2025) (https://lmsys.org/blog/2025-09-22-sglang-deterministic/)
3. SGLang Documentation: Deterministic Inference (https://docs.sglang.io/advanced_features/deterministic_inference.html)
4. NVIDIA Developer Blog. "Optimizing for Low-Latency Communication in Inference Workloads with JAX and XLA" (2025) (https://developer.nvidia.com/blog/optimizing-for-low-latency-communication-in-inference-workloads-with-jax-and-xla/)
5. JAX Documentation. "GPU Performance Tips" (https://docs.jax.dev/en/latest/gpu_performance_tips.html)

Code Availability

Complete implementation: github.com/dtunai/batch-invariant-ops-jax

• plaintextCopy

  ops/rmsnorm_batch_invariant_op.py

  : Invariant RMSNorm
• plaintextCopy

  ops/matmul_batch_invariant_op.py

  : Fixed-tile MatMul
• plaintextCopy

  fp_nonassociativity.py

  : Floating-point demonstrations

See you in Learning Log 2, where we will explore batch-invariant attention.